Answer:

Explanation:
What we want to find here is the arc length of 1/2 of a circle, we'll start by finding the of the circle.
Step 1:- find the circumference of the circle →



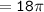
Step 2:- find the arc length of 1/2 of the circle →
The arc length is 1/2 of the circumference of the circle:-

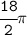

Therefore, the arc length of the semicircle is 9π.