Answer:
The time it takes the ball to land on green is 4.4175 seconds
Explanation:
Given
Equation for number of seconds it take to hit the green: −16t² + 70t + 6 = −3
Required
The value of t.
The interpretation of this question is that, we should solve for t in the above equation.
-16t² + 70t + 6 = −3
Collect like terms
-16t² + 70t + 6 - 3 = 0
-16t² + 70t + 3 = 0
Multiply through by -1
-1(-16t² + 70t + 3) = -1 * 0
16t² - 70t - 3 = 0
Solving using quadratic formula.
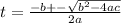
Where a = 16, b = -70, c = -3
t = (-(-70) ± √(-70² - 4 * 16 * -3))/(2 * 16)
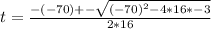
t = (70 ± √(4900 + 192))/32
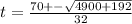

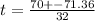
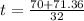 or
or

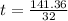 or
or
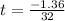
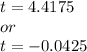
But t can't be negative.
So, t = 4.4175
The time it takes the ball to land on green is 4.4175 seconds