Question

Please help me with these two algebra questions. Image attached.

Answer 1

1. when x⇒∞, y=∞ and when x⇒-∞, y=-∞

So, we have a odd degree polynomial (x³ or
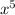`x^5` or even
`x^9`).

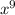The leading coefficient is negative its end behavior matches x³ which has a positive leading coefficient.

2. when x⇒∞, y=∞ and when x⇒-∞, y=∞

So, we have a even degree polynomial (x² or
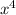`x^4` or even
`x^(100)`).

And because it matches these parent functions listed above (they all have positive leading coefficients), the leading coefficient is again positive.

answers:

1. odd and positive

2. even and positive