Question

A researcher wanted to test the claim that, "Seat belts are effective in reducing fatalities." A simple random sample of front-seat occupants involved in car crashes is obtained. Among 2823 occupants not wearing seat belts, 31 were killed. Among 7765 occupants wearing seat belts, 16 were killed. If a significance level of 5% is used, which of the following statements gives the correct conclusion?

A) Since p >a we conclude that this data shows that seat belts are effective in reducing fatalities.
B) Since p C) Since p >o we conclude that this data shows that seat belts aren't effective in reducing fatalities.
D) Since p

Answer 1

`z = \frac{0.00206 -0.0110}{\sqrt{(0.00206*(1-0.00206))/(7765) +(0.0110*(1-0.0110))/(2823)}}= -4.405`

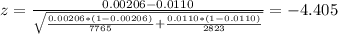
Now we can find the p value since we are using a left tailed test the p value would be:

`p_v = P(z<-4.405)=0.00000529`

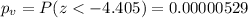
Since the p value is very low compared to the significance level of 0.05 we have enough evidence to reject the null hypothesis and then the best conclusion would be:

B) Since p <a, we conclude that this data shows that seat belts are effective in reducing fatalities.

Explanation:

We have the following info given from the problem

`X_1 =31` number of people killed with occupants not wering seat belts

`n_1 = 2823` number of people not wearing seat belts

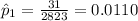`\hat p_1 =(31)/(2823)=0.0110` represent the estimated proportion of people killed not wearing seatbelts

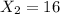`X_2 =16` number of people killed with occupants using wering seat belts

`n_2 = 7765` number of people using wearing seat belts

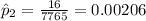`\hat p_2 =(16)/(7765)=0.00206` represent the estimated proportion of people killed wearing seatbelts

We want to check if seat belts are effective in reducing fatalities, so we want to test the following system of hypothesis:

Null hypothesis:
`p_2 \geq p_1`

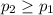
Alternative hypothesis:
`p_2 <p_1`

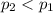
The statistic for this case is given by:

`z = \frac{\hat p_2 -\hat p_1}{\sqrt{(\hat p_1 (1-\hat p_1))/(n_1) +\hat p_2 (1-\hat p_2)}{n_2}}}`

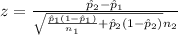
And replacing we got:

`z = \frac{0.00206 -0.0110}{\sqrt{(0.00206*(1-0.00206))/(7765) +(0.0110*(1-0.0110))/(2823)}}= -4.405`

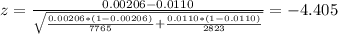
Now we can find the p value since we are using a left tailed test the p value would be:

`p_v = P(z<-4.405)=0.00000529`

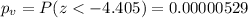
Since the p value is very low compared to the significance level of 0.05 we have enough evidence to reject the null hypothesis and then the best conclusion would be:

B) Since p <a, we conclude that this data shows that seat belts are effective in reducing fatalities.