Question

The Pew Research Center reported that 73% of Americans who own a cell phone also use text messaging. In a recent local survey, 155 out of 200 cell phone owners used text messaging.

Since a Z test is appropriate, test whether the population proportion of Americans who use text messaging is different from 73%. Use level of significance α = 0.10.
Hint: Do you need to conduct a t-test or a z-test? Next, find the p-value, using p-value, and level of significance, you can see if the decision (Reject or Do Not reject H0.) You can also find the critical value(s) to finalize your decision.

Answer 1

`z=\frac{0.775 -0.73}{\sqrt{(0.73(1-0.73))/(200)}}=1.433`

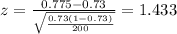
Now we can find the p value. Since we have a bilateral test the p value would be:

`p_v =2*P(z>1.433)=0.152`

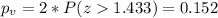
Since the p value is higher than the significance level of 0.1 we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case would be:

Do Not reject H0

Explanation:

Information provided

n=200 represent the sample size slected

X=155 represent the cell phone owners used text messaging

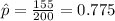`\hat p=(155)/(200)=0.775` estimated proportion of cell phone owners used text messaging

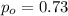`p_o=0.73` is the value to verify

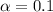`\alpha=0.1` represent the significance level

We need to conduct a z test for a proportion

z would represent the statistic

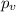`p_v` represent the p value

System of hypothesis

We want to verify if the true proportion of cell phone owners used text messaging is different from 0.73 so then the system of hypothesis are:

Null hypothesis:
`p=0.73`

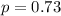
Alternative hypothesis:
`p \\eq 0.73`

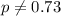
The statistic to check this hypothesis is given by:

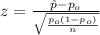`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the data given we got:

`z=\frac{0.775 -0.73}{\sqrt{(0.73(1-0.73))/(200)}}=1.433`

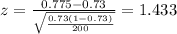
Now we can find the p value. Since we have a bilateral test the p value would be:

`p_v =2*P(z>1.433)=0.152`

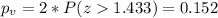
Since the p value is higher than the significance level of 0.1 we have enough evidence to FAIL to reject the null hypothesis and the best conclusion for this case would be:

Do Not reject H0