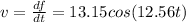Question

You wiggle a string,that is fixed to a wall at the other end, creating a sinusoidalwave with a frequency of 2.00 Hz and an amplitude of 0.075 m. Thespeed of the wave is 12.0 m/s. At t=0 the string has a maximum displacementand is instantaneously at rest.Assume no waves bounce back from the far end of the wall. Find the angular frequency, period, wavelength,and wave number. Write a wave function describingthewave. Write equations for the displacement, as a function of time, of the end of the string that is being wiggled and at a point 3.00 m from that end. Determine the speed of the medium and draw history and snapshot graphs for the waves created.

Answer 1

Step-by-step explanation:

A general wave function is given by:

`f(x,t)=Acos(kx-\omega t)`

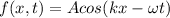
A: amplitude of the wave = 0.075m

k: wave number

w: angular frequency

a) You use the following expressions for the calculation of k, w, T and λ:

`\omega = 2\pi f=2\pi (2.00Hz)=12.56(rad)/(s)`

`k=(\omega)/(v)=(12.56(rad)/(s))/(12.0(m)/(s))=1.047\ m^(-1)`

`T=(1)/(f)=(1)/(2.00Hz)=0.5s\\\\\lambda=(2\pi)/(k)=(2\pi)/(1.047m^(-1))=6m`

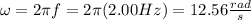
b) Hence, the wave function is:

`f(x,t)=0.075m\ cos((1.047m^(-1))x-(12.56(rad)/(s))t)`

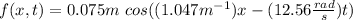
c) for x=3m you have:

`f(3,t)=0.075cos(1.047*3-12.56t)`

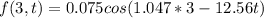
d) the speed of the medium:

`(df)/(dt)=\omega Acos(kx-\omega t)\\\\(df)/(dt)=(12.56)(1.047)cos(1.047x-12.56t)`

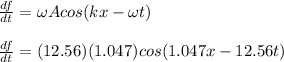
you can see the velocity of the medium for example for x = 0:

`v=(df)/(dt)=13.15cos(12.56t)`