Answer:
23.4 units
Explanation:
Given the point of the vertices of triangle ABC as A(−5,1), B(2,1), and C(6,4).
The distance (d) between two points X (x₁ , y₁) and Y(x₂, y₂) is given as:
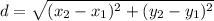 . We can use this to calculate the length of the sides of the triangle. Therefore:
. We can use this to calculate the length of the sides of the triangle. Therefore:
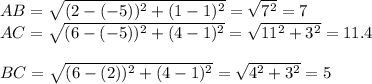
The perimeter of the triangle ABC = AB + AC + BC = 7 + 11.4 + 5 = 23.4 units