Question

The first step in solving a system of linear equations using a graph is to write the

equations in a form that is easy to graph. Explain the next steps to solving and checking
the solution.
(#4) ASAP PLS

Answer 1

I've spotted a mistake, so I'll start with fixing that.

In 1., it asks you for a system of equations. It should be:

`x + y = 165 \\ 10x + 7y = 1440`

Yes, with two equations, as it is unsolvable otherwise.

Then, on 2., you need to solve the system:

`10x+ 7(165 - x) = 1440 \\10x + 1155 - 7x = 1440 \\ 3x = 1440 - 1155 \\ 3x = 285 \\ x = 95`

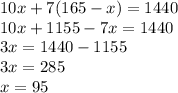
This is the way to get to 95 without graphing (obviously, by graphing, the x coordinate of the intersection would be the solution).

For 3, go back to the system, and solve for y:

`x + y = 165 \\ 95 + y = 165 \\ y = 165 - 95 \\ y = 70`

The answer for 3 would be (95,70). Only that. Straight lines can only intersect a maximum of 1 time.

Finally, for 4:

After modelling a system, and converting the equations to slope-intercept format, for easier graphing, the equations are plotted. Hopefully, the lines intersect each other at some point, giving us the solution as (x,y). We can then replace the variables in the equations in the system, to check for equality. If the lines do not intersect, then there is no solution to the system.

Again, this answer is broad, and it is meant to have you understand the topic more deeply.