Question

Mandy drew a regression line for this paired data set.

Her line passed through (2, 9) and (4, 5).
What is the equation of Mandy's regression line?
Enter your answer, in slope-intercept form, in the box.

Answer 1

yˆ=1.5x+0.5

Explanation:

Answer 2

The equation of Mandy's regression line for the given paired data set is y = -2x + 13.

Calculate the slope (m):

To find the slope, we can use the formula:
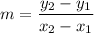`$m = \frac{{y_2 - y_1}}{{x_2 - x_1}}$`, where
`$(x_1, y_1)$` and
`$(x_2, y_2)$` are two points on the line.

Using the given points (2,9) and (4,5), we have:

`$m = \frac{{5 - 9}}{{4 - 2}} = \frac{{-4}}{{2}} = -2$`

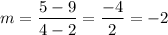
Substitute the slope and one of the given points into the equation:

We can use either point (2,9) or (4,5) in the equation y = mx + b.

Using point (2,9):

9 = -2(2) + b

Simplifying the equation, we get:

9 = -4 + b

b = 9 + 4 = 13

Write the equation of the regression line:

Now that we have the slope (m = -2) and the y-intercept (b = 13), we can write the equation of Mandy's regression line:

y = -2x + 13