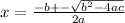Question

Describe the steps that are necessary before plugging the following Quadratic Equation into the Quadratic Formula: x2 = -8x + 48. (Hint: There are 3 steps prior to plugging in)

Answer 1

move the -8x to the left side as a +8x

move the 48 as a -48 to the left side

identify a, b, and c.

Explanation:

the expression is:

`x^2=-8x+48`

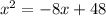
to be able to plug the values for the quadratic formula, we need all of the terms on one side of the equal sign. Thus the first step is:

move the -8x to the left side as a +8x:

`x^2+8x=48`

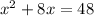
second step:

move the 48 as a -48 to the left side:

`x^2+8x-48=0`

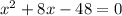
third step:

identify a, b, and c.

a is the number that accompanies the
`x^2`

`a=1`

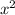
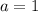
b is the number that accompanies the
`x`

`b=8`

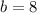
and c is the indepedent number:

`c=-48`

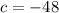
Now you are ready to plug these number into the quadratic formula:

`x=(-b+-√(b^2-4ac) )/(2a)`