Question

* Pls I’m being timed *

Find the approximate perimeter of VEN plotted below.
Round your final answer to the nearest hundredth.

Answer 1

≈ 29.03

Explanation:

from the photo, we can find the coordinates of the 3 points are:

• V (1, 7)
• E (-3, -4)
• N (5, 7)

To find the approximate perimeter of VEN, we need to know the lenght of 3 sides. Let's find them:

As we know, the distance of two points can be determined by this formula:
`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

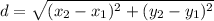
So that, the distance of:

VN =
`√((5-1)^2+(7-7)^2) = \sqrt{4^(2) } = 4`

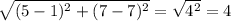
EN =
`√((5-(-3))^2+(7-(-4))^2) = \sqrt{8^(2)+11^(2) } =√(185)`

EV =
`√((1-(-3))^2+(7-(-4))^2) = \sqrt{4^(2)+11^(2) } =√(137)`

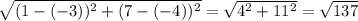
=> the approximate perimeter of VEN is:

VN + EN + EV

= 4 +
`√(185) + √(137)`

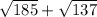
≈ 29.03