Question

Math question quadratics

Answer 1

(y1, y2)= (30,50)

(x1, x2)= (50,30)

If x is the length, it would be 50 m, y (width) would be 30 m

It depends on the way you determine x and y

Explanation:

The perimeter of the pool:

(x+y)*2= 160

So the total length and width of the pool is:

x+y = 80 (1)

The area of the pool:

xy= 1500 (2)

(1), (2) =) x+y=80

xy= 1500

=) y= 80-x

x (80-x) =1500

=) y= 80-x

80x -x² = 1500

=) y= 80 -x

x² - 80x +1500=0

=) y1= 80- 50 y2= 80-30

(x1, x2)= (50,30)

=) (y1, y2)= (30,50)

(x1, x2)= (50,30)

Answer 2

Answer: The length and width are 50 and 30 meters (or 30 and 50 meters).

Explanation:

To solve this question, we can represent variables for the length and width in two equations.

`2l + 2w = 160\\\\l * w= 1500`

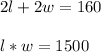
To solve for one of the variables, you'll have to substitute one of the variables, so solve for one of them:

`2l = 160 - 2w\\l = 80 - w`

`(80-w)*w=1500\\\\-w^2 + 80w - 1500 = 0\\\\w^2 - 80w + 1500 = 0`

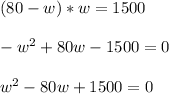
Now, we have a standard quadratic equation that we can factor. When factoring, you'll get this:

`(w-50)(w-30) = 0`

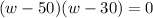
This tells us that the width could be either 50 or 30.

Substitute 50 into one of the equations to find the length:

2 (l) + 100 = 160

l = 30.

The length and width are 50 and 30 meters (or 30 and 50 meters).