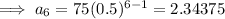Answer:
442.96875 ft
Explanation:
We can model the height of each bounce as a geometric series.
General form of a geometric sequence:

(where
 is the initial term and
is the initial term and
 is the common ratio)
is the common ratio)
If we let n be the number of bounces, then the initial term has to be:

since this is the height of the ball after the first bounce.
The common ratio r has already been given to us, as we have been told that the height of the bounce halves after each bounce.
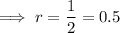
Therefore, the geometric series to model the peak height of each bounce is:
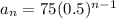
(where
 is the height and n is the number of bounces)
is the height and n is the number of bounces)
Therefore, to calculate the total number of feet the ball travels until it reaches the peak height of the 6th bounce:
Total = 150 + (2 × sum of 1, 2, 3, 4 & 5th bounces) + 6th bounce
To find the sum, use the geometric sum formula:
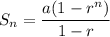
Therefore, the sum of the bounces 1 through 5 is:

Height of the 6th bounce: