Question

Find the absolute maximum and absolute minimum values of the function f(x)=x3+6x2−63x+9 over each of the indicated intervals. (a) Interval = [−8,0]. 1. Absolute maximum = -99 2. Absolute minimum = 9 (b) Interval = [−5,4]. 1. Absolute maximum = 348 2. Absolute minimum = -100 (c) Interval = [−8,4]. 1. Absolute maximum = 400 2. Absolute minimum =

Answer 1

a) The absolute maximum is 401 and the absolute minimum is 9.

b) The absolute maximum is 349 and the absolute minimum is -99.

c) The absolute maximum is 401 and the absolute minimum is -99.

Explanation:

The absolute minimum and absolute maximum values are determined with the help of the First and Second Derivative Tests:

FDT

`3\cdot x^(2) + 12\cdot x - 63 = 0`

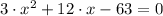
The roots of the function are:
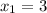`x_(1) = 3` and
`x_(2) = -7`. Each point is evaluated in the second derivative of the function:

SDT

`f''(x) = 6\cdot x + 12`

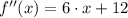
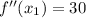`f''(x_(1)) = 30` (Absolute minimum)

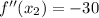`f''(x_(2)) = -30` (Absolute maximum)

The values for each extreme are, respectively:

`f(x_(1)) = -99`

`f(x_(2)) = 401`

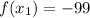
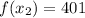
Now, each interval is analyzed herein:

a) The absolute maximum is 401 and the absolute minimum is 9.

b) The absolute maximum is 349 and the absolute minimum is -99.

c) The absolute maximum is 401 and the absolute minimum is -99.