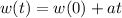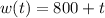Question

The water level of a lake has been increasing each year. The initial water level of the lake was 800 meters, and the water level increases by 1 m each year. Use this information to answer the questions below.

Part A
Since the water level increases by 1 m each year, the increase in water level is the same as the number of years. Write an equation relating final water level (w) to the time in years (t).


(i need help like rn)

Answer 1

`w(t) = 800 + t`

Explanation:

Since the increase is the same each year, we can model this situation by a linear function, in the following format:

`w(t) = w(0) + at`

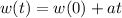
In which w(t) is the water level after t years, w(0) is the initial water level and a is the yearly increase.

The initial water level of the lake was 800 meters

This means that
`w(0) = 800`

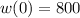
The water level increases by 1 m each year.

This means that
`a = 1`

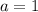
So

`w(t) = w(0) + at`

`w(t) = 800 + t`