Answer:
( x + 5 )² + ( y - 3 )² = 52
Explanation:
Let find the equation of the line going through A( - 11, 7 ) and B( - 9, - 3 )
m =
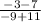 = - 5
= - 5
y - 7 = - 5( x + 11 )
y = - 5x - 48
Now, let find the equation of the line passing through midpoint of the segment AB
Coordinates of that midpoint is (
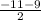 ,
,
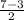 ) = ( - 10 , 2 )
) = ( - 10 , 2 )
Slope of the perpendicular line is
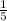 ( opposite reciprocal of ( - 5 )
( opposite reciprocal of ( - 5 )
y - 2 =
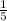 ( x + 10 )
( x + 10 )
y =
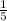 x + 4 ........... (1)
x + 4 ........... (1)
Coordinates of an intersection of two lines (1) and x = - 5 are coordinates of the center of the circle
y =
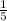 ( - 5 ) + 4 = 3 ⇒ y = 3
( - 5 ) + 4 = 3 ⇒ y = 3
O( - 5 , 3 ) is the center
The last!! RADIUS which is OA or OB
r =
 = √52
= √52
( x + 5 )² + ( y - 3 )² = 52