Question

A physics instructor wants to produce a double-slit pattern large enough for her class to see. For the size of the room she decides that the distance between successive bright fringes on the screen should be at least 1.5 cm. If the slits have a separation of distance of 34 m what is the minimum distance from the slits to the screen when 632.8 nm light is used?

Answer 1

80 cm

Step-by-step explanation:

To find the minimum distance from the slits to the screen you use the following formula for the m-th fringe of the interference pattern:

`y=(m\lambda D)/(d)`

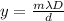
m: order of the fringe

λ: wavelength = 632.8*10^-9 m

D: distance to the screen

d: distance between slits = 0.034*10^-3

for the distance between fringes you have:

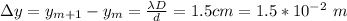`\Delta y=y_(m+1)-y_m=(\lambda D)/(d)=1.5cm=1.5*10^(-2)\ m` ( 1 )

By replacing the values of the parameters in (1) you can find the distance D to the screen:

`D=(\Delta y d)/(\lambda)=((1.5*10^(-2)m)(0.034*10^(-3)m))/(632.8*10^(-9)m)=0.80m=80\ cm`

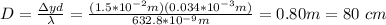
hence, the distance from the slits to the screen is 80 cm