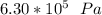Question

A bicycle tire has a pressure of 6.9 × 105 Pa at a temperature of 17.5°C and contains 2.00 L of gas. show answer Incorrect Answer What will its pressure be, in pascals, if you let out an amount of air that has a volume of 95 cm3 at atmospheric pressure and at the temperature of the tire? Assume tire temperature and volume remain constant. P2 = 14526315.79| sin() cos() tan() cotan() asin() acos() atan() acotan() sinh() cosh() tanh() cotanh() Degrees Radians π ( ) 7 8 9 HOME E ↑^ ^↓ 4 5 6 ← / * 1 2 3 → + - 0 . END √() BACKSPACE DEL CLEAR Grade Summary Deductions 8% Potential 92% Submissions Attempts remaining: 1 (4% per attempt) detailed view 1 4% 2 4%

Answer 1

the final pressure in pascal =
`6.30*10^5 \ \ Pa`

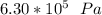
Step-by-step explanation:

Given that:

initial pressure =
`6.9*10^5 \ Pa`

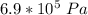
Initial Temperature = 17.5 °C = (17.5 + 273) K = 290.5 K

Volume = 2.00 L = 2.00 × 10⁻³ m³

Initial volume of the air occupied by gas V' = 95 cm³ = 95× 10⁻⁶ m

Using the ideal gas temperature;

PV = nKT

where

K = Boltzmann constant = 1.38 × 10⁻²³

From above expression;

`n = (PV)/(KT)`

`n = (6.9*10^5*2.00*10^(-3))/(1.38*10^(-23)*290.5)`

`n = 3.44*10^(23)`

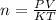
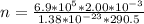
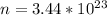
The number of moles that were removed from the tire is calculated as

`\Delta \ n = (P_(atm)*V')/(KT)`

where

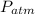`P_(atm)` = atmospheric pressure =
`1.013*10^5`

`\Delta \ n = (1.013*10^5*95*10^(-6))/(1.38*10^(-23)*290.5)`

`\Delta \ n = 2.4*10^(21)`

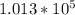
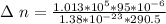
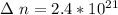
The remaining number of moles after the release of gas is

`n_2 = n- \Delta n`

`n_2 = 3.44*10^(23) -2.4*10^(21)`

`n_2 = 3.416*10^(23)`

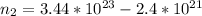
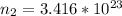
Using the expression
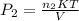`P_2 = (n_2 KT)/(V)` to determine the final pressure:

`P_2 = (3.416*10^(23)*1.38*10^(-23)*290.5 )/(2.00*10^(-3))`

`P_2 = 6.30*10^5 \ \ Pa`

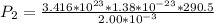
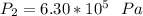
Hence, the final pressure in pascal =
`6.30*10^5 \ \ Pa`