Answer:
a. 385
b. 342
Explanation:
To solve the problem we do the following:
The equation to calculate the sample size is:
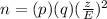
a)
We have the following data:
Since no estimate of proportion is given, we will assume: p = q = 0.5
We know that For 95% confidence, z = 1.96
Width = 0.10
Hence, the margin of error would be:
0.10 / 2 = 0.05
E = 0.05
And so we can calculate sample size:
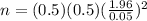
n = 385
b)
We have the following data for this point:
p = 2/3
q = 1 - p
q = 1 - 2/3
q = 1/3
And so we can calculate sample size:
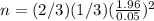
n = 342