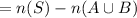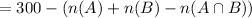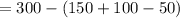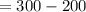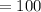2 Answers

Linktoahref · Answer 1 · 2021-07-16T17:32:14+0000

Answer:100

Explanation:

Suppose S is the set of number of first 300 natural number

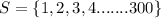
$S=\{1,2,3,4.......300\}$

And A be the set of number divisible by 2

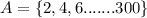
$A=\{2,4,6.......300\}$

so total element in A is
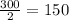
(300)/(2)=150

Let B be the set containing the element divisible by 3

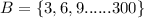
$B=\{3,6,9......300\}$

So element in B is
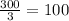
(300)/(3)=100

But there are some element which is common in both A and B

so
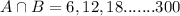
$A\cap B={6,12,18.......300}$

Element in
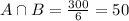
$A\cap B=(300)/(6)=50$

and so number of elements which are less than 300 and neither divisible by 2 nor 3 is

$=n(S)-n(A\cup B)$

$=300-(n(A)+n(B)-n(A\cap B))$

=300-(150+100-50)

=300-200

=100

Please log in or register to add a comment.