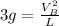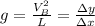Question

A uniform, thin rod of length L and mass M is allowed to pivot about its end. The rotational inertia of a rod about its end is ML2/3. The rod is fixed at one end and allowed to fall from the horizontal position through the vertical position. The student has a variety of rods of various lengths that all have a uniform mass distribution. Design an experiment that the student could conduct to find an experimental value of g.

Answer 1

`g = (V_B^2)/(L) = (\Delta y)/(\Delta x)`

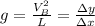
Step-by-step explanation:

Given that :

length of the thin rod = L

mass = m

The rotational inertia I =
`(ML^2)/(3)`

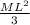
The experimental design that the student can use to conduct the experimental value of g can be determined as follow:

Taking the integral value of I

`I =\int\limits \ r^2 \, dm`

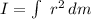
where :

`\lambda = (m)/(L) \\ \\ m = L \lambda \\\\ \lambda dr = dm`

`I =\int\limits^L_0 { \lambda r^2 } \, dr`

`I = (\lambda r^3)/(3) |^L___0`

`I = (m)/(3 L)L^3`

`I = (1)/(3 )mL^2`

`k_f = \mu___0}}} = \frac{1}2} I \omega^2`

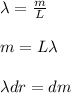
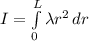
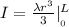
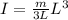
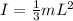
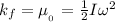
where:

`V_B = \omega L`

`\omega = (V_B)/(L)`

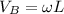
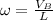
Equating:
`\frac{1}2} I \omega^2 = mg (L)/(2)`; we have:

`(1)/(2) ((1)/(3)mL^2)(V_B^2)/(L^2) = mg (L)/(2)`

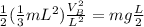
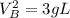`V_B^2 = 3gL` since m = 3g

where :

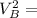`V_B^2 =`vertical axis on the graph

L = horizontal axis

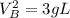`V_B^2 = 3gL` ( y = mx)

`3g = (V_B^2)/(L)`

`g = (V_B^2)/(L) = (\Delta y)/(\Delta x)`