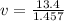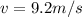Question

Greg throws a 2.8-kg pumpkin horizontally off the top of the school roof in order to hit Mr. H's car. The car has parked a distance of 13.4 m away from the base of the building below the point where Greg is standing. The building's roof is 10.4 m high. Assuming no air resistance, with what horizontal speed does Greg toss the pumpkin in order to hit Mr. H's car

Answer 1

The horizontal velocity is
`v = 9.2 m/s`

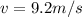
Step-by-step explanation:

From the question we are told that

The mass of the pumpkin is
`m = 2.8 \ kg`

The distance of the the car from the building's base is
`d = 13.4 \ m`

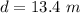
The height of the roof is
`h = 10.4 \ m`

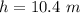
The height is mathematically represented as

`h = (1)/(2) gt^2`

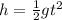
Where g is the acceleration due to gravity which has a value of
`g =9.8 \ m/s^2`

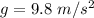
substituting values

`10.4= 0.5 * 9.8 * t`

making the time taken the subject of the formula

`t = (10.4)/(0.5 * 9.8 )`

`t = 1.457 \ s`

The speed at which the pumpkin move horizontally can be represented mathematically as

`v = (d)/(t)`

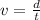
substituting values

`v =(13.4)/(1.457)`

`v = 9.2 m/s`