Answer:
Step-by-step explanation:
So; in this question I figured out that there are different types of question embedded in the question.
For the first part :
Suppose a monopolist faces the market demand function P = a - bQ. Its marginal cost is given by MC = c + eQ. Assume that a > c and 2b + e > 0. a) (2 marks) Derive an expression for the monopolist’s optimal quantity and price in terms of a, b, c, and e.
Given that:
The market demand function is:
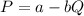
and it marginal cost is
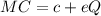
So ;

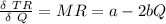
Then for the expression for the monopolist’s optimal quantity and price in terms of a, b, c, and e: we have;

∴
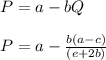
For the second part of the question:
Market demand is P = 64 - (Q/7). A multiplant monopolist operates three plants, with marginal cost functions: a) (2 marks) Find the monopolist’s profit-maximizing price and output at each plant. b) (2 marks) How would your answer to part (a) change if MC2 (Q2) = 4?
Given that:
The market demand is P = 64 - Q/7, then MR = TR' = 64 - 2/7Q.
In equilibrium MR = MC:
a)
MC1(Q1) = 4Q = 64 - 2/7Q,
Q = 64×7/9
Q = 49.78 units.
P = 64 - 49.78/7
P = 56.9
MC2(Q2) = 2 + 2Q = 64 - 2/7Q,
Q = 62×7/16
Q = 27.1 units.
P = 64 - 27.1/7
P = 60.1
MC3(Q3) = 6 + Q = 64 - 2/7Q,
Q = 58×7/9
Q = 45.1 units.
P = 64 - 45.1/7
P = 57.6
b)
Given that :
MC2 (Q2) = 4, then:
64 - 2/7Q = 4,
Q = 60×7/2 = 210 units.
P = 64 - 210/7 = 34
For the third part ; which is the final section of the question:
Consider a market in which the market demand curve is given by P = 18 - X - Y, where X is Firm 1’s output, and Y is Firm 2’s output. Firm 1 has a marginal cost of 3, while Firm 2 has a marginal cost of 6. a) (2 marks) Find the Cournot equilibrium outputs in this market. How much profit does each firm make? b) (2 marks) Find the Stackelberg equilibrium in which Firm 1 acts as the leader. How much profit does each firm make?
a)
Cournot Equilibrium for firm 1:
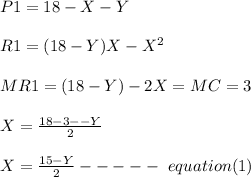
For Firm 2 :
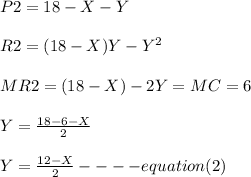
Replacing the parameters for Y in equation (1); we have :
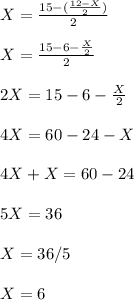
From equation (2) ; substitute the value of X = 6; we have:
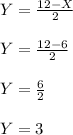
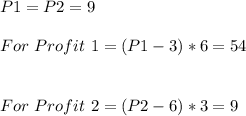
b) For Stackelberg equilibrium :
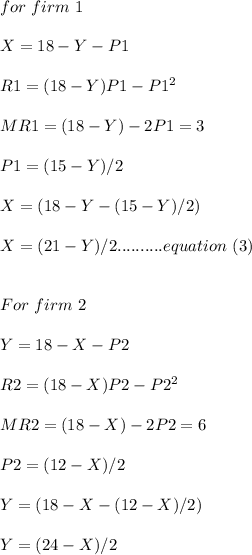

I hope that helps a lot!