Answer:
67.80 mL
Step-by-step explanation:
The heat q is given by the formula:
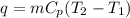
Since heat released by the coffee = - heat absorbed by the milk; Then :
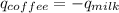
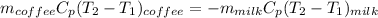
From the question;
given that the heat capacity of milk & coffee are equal; The density are also said to be equal:
The temperature difference for coffee is as follows:
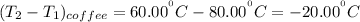
Temperature difference for milk is :
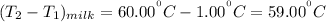
We all know that : Density
 = mass (m) / volume (v)
= mass (m) / volume (v)
then m = v ×

So, we can say that :
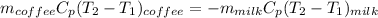 can now be re-written as:
can now be re-written as:
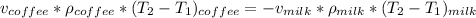
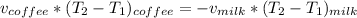
Replacing the values; we have :
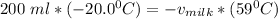
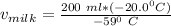
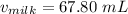
Therefore, the amount of milk required to reach the required temperature for coffee is 67.80 mL