Answer:
4.96*10^-20 J
Step-by-step explanation:
To find the average electromagnetic energy of the wave you use the fact that the wave can be taken as a spherical electromagnetic wave. IN this case, the amplitude of the wave change in space according to:
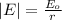
for a distance of 8.5km = 5.5*10^3m you have:
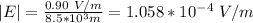
Next, to find the average energy at this point you use the following formula:
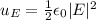
εo : dielectric permittivity of vacuum = 8.85*10^-12C^2/Nm^2
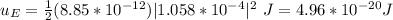
hence, the average energy of the wave is 4.96*10^-20 J