Question

In the diagram shown on circle A, segment CD is tangent to the circle at point D. If CD=23 and CA = 28.

then which of the following is closest to mZC?

Answer 1

35°

Explanation:

The diagram is shown in the image attached.

A tangent is a line that intercepts at one unique point. When we have a tangent about a circle, an important results is that the tangent is perpendicular to the radius, because a radius can be seen as perpendicular to any point of the circle.

That means, the triangle formed ADC is a right triangle, because
`\angle D= 90\°`.

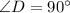Now, we know that
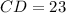`CD=23` and
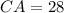`CA=28`, which are leg and hypothenuse, respectively.

So, to find
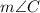`m \angle C` we just need to use trigonometric reasons, specifically, the cosine funtion, because it relates the adjacent leg and the hypothenuse.

`cos(C)=(CD)/(CA)=(23)/(28) \\C=cos^(-1)((23)/(28) ) \approx 35 \°`

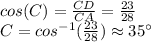
Therefore, the measure of angle C is 35°, approximately.