Answer: (a) t = 20.36.
 s
s
(b) d = 60.225 m
Explanation: According to the Special Relativity Theory proposed by Albert Einstein, the laws of physics are the same for all non-accelerating observers and speed of light is the same in vaccum, no matter the speed the pbserver is travelling. with these statements, Einstein realized that space and time interwoven in a continuum called space-time, i.e., events that occur for one observer at the same time, occurs at different times for a second observer.
(a) To determine the lifetime and since the person is riding along:
t =
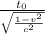 , in which:
, in which:
t is time observed in the other time frame
t₀ is time in the observer's own reference
v is velocity of the object
c is the speed of light in vacuum (c=3.
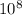 m/s)
m/s)
Calculating:
t =
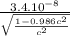
t =
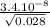
t = 20.36.

The lifetime, according to the hypothetical person is 20.36.
 seconds.
seconds.
(b) The pion is moving at a speed of v = 0.986c. In 20.36 seconds,
the laboratory moves:
v=

d = v.t
d = 0.986.3.
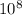 .20.36.
.20.36.

d = 60.225
The lab moved 60.225 meters.