Answer:
97 adults and 151 children assisted to that show.
Explanation:
We are gonna use "dollars" instead of "soles.
According to the problem, tickets cost $30 for adults and $20 for children.
Last Saturday assisted 248 people which gave a total of $5930.
To know the number of adults and children were there, we need to defined a system of equations.
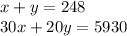
Where
 represents adults and
represents adults and
 represents children.
represents children.
First, we multiply the first equation by -20
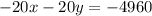
Then, we sum this equation with the second one
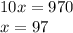
There were 97 adults.
Now, we use this value to find the other one
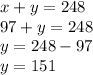
There were 151 children.
Therefore, 97 adults and 151 children assisted to that show.