Answer:
There is enough evidence to reject the manufacturer’s claim and the standardized test statistic z is -3.43
Explanation:
A manufacturer of sprinkler systems designed for fire protection claims that the average activating temperature is at least 135°F.
So, Null hypothesis:

Alternate hypothesis :
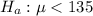
To test this claim, you randomly select a sample of 32 systems and find the mean activation temperature to be 133°F.
x=133
n = 32
Population Standard deviation =
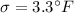
Formula :

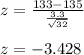
z=-3.43
Refer the z table for p value
p value = 0.0003
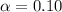
p value < α
So, we failed to accept null hypothesis
Hence there is enough evidence to reject the manufacturer’s claim and the standardized test statistic z is -3.43