Answer:
the magnitude of the magnetic field is 8.704 x 10⁻⁴ T
Step-by-step explanation:
Given;
potential difference, V = 278 V
radius of the circular path, r = 6.46 cm = 0.0646 m
charge of electron, q = 1.60218 × 10⁻¹⁹ C
mass of electron, m = 9.10939 × 10⁻³¹ kg
The magnitude of the magnetic field is given as;

where;
B is the magnitude of the magnetic field
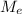 is mass of the electron
is mass of the electron
v is velocity of the electron
r is the radius of the circular path
q is charge of the electron
Determine velocity of the electron from kinetic energy equation;

the magnitude of the magnetic field:
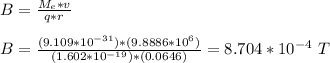
Therefore, the magnitude of the magnetic field is 8.704 x 10⁻⁴ T