Question

We will look at an example of a banked curve. In this case the normal force provides the needed radial acceleration. This allows the vehicle to negotiate the curve without having to rely solely on friction. An engineer proposes to rebuild the curve, banking it so that, at a certain speed v, no friction at all is needed for the car to make the curve. At what angle β should the curve be banked if v = 25 m/s, (56 mi/h) and R=250m?

Answer 1

The bank angle
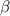`\beta\\` = 14.30 degrees

Step-by-step explanation:

In engineering, banking a curve reduces the centripetal force on the cars as they turn round the bend. this helps prevent them from sliding off the road.

The bank angle can be calculated using the formula:

`tan \beta =(v^(2))/(gR)`

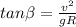
where v = velocity of the car = 25 m/s

R = radius of the bank = 250 m

g = acceleration due to gravity =
`9.81 m/s^(2)`

`tan \beta =(25^(2))/(9.81 * 250)`

`tan\beta =0.25484`

`\beta = tan^(-1) (0.25484)= 14.30 degrees`

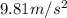
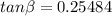
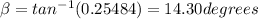
There fore, the bank angle is approximately 14 degrees