Question

A pulley with a radius of 3.0 cm and a rotational inertia of 4.5 x 10–3 kg∙m2 is suspended from the ceiling. A rope passes over it with a 2.0-kg block attached to one end and a 4.0-kg block attached to the other. The rope does not slip on the pulley. When the velocity of the heavier block is 2.0 m/s the total kinetic energy of the pulley and blocks is:

Answer 1

22J

Step-by-step explanation:

Given :

radius 'r'= 3cm

rotational inertia 'I'=4.5 x
`10^(-3)` kgm²

mass on one side of rope '
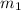`m_{1`'= 2kg

mass on other side of rope'
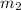`m_{2`' =4kg

velocity'v' of mass
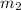`m_{2`' = 2m/s

Angular velocity of the pulley is given by

‎ω = v /r => 2/ 3x
`10^{-2`

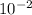
‎ω = 66.67 rad/s

For the rotating body, we have

KE =
`(1)/(2)` I ω²

`KE_p = (1)/(2) (4.5 *10^(-3) )(66.67^(2) )`

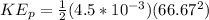
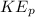`KE_p` = 10J

Next is to calculate kinetic energy of the blocks :

`KE_(b) = (1)/(2) (m_1 + m_2).v^2\\KE_b= (1)/(2) (2+4).2^2`

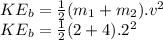
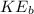`KE_b`=12J

Therefore, the total kinetic energy will be

KE =
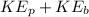`KE_p + KE_b` =10 + 12

KE= 22J