Answer:
We conclude that the vaccine appears to be effective.
Step-by-step explanation:
We are given that a doctor released the results of clinical trials for a vaccine to prevent a particular disease.
The subjects in group 1 (the experimental group) were given the vaccine, while the subjects in group 2 (the control group) were given a placebo. Of the 200 comma 000 children in the experimental group, 38 developed the disease. Of the 200 comma 000 children in the control group, 81 developed the disease.
Let
 = proportion of subjects in the experimental group who developed the disease.
= proportion of subjects in the experimental group who developed the disease.
 = proportion of subjects in the control group who developed the disease.
= proportion of subjects in the control group who developed the disease.
So, Null Hypothesis,
 :
:
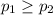 {means that the vaccine does not appears to be effective}
{means that the vaccine does not appears to be effective}
Alternate Hypothesis,
 :
:
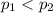 {means that the vaccine appears to be effective}
{means that the vaccine appears to be effective}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
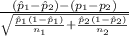 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of children in the experimental group who developed the disease =
= sample proportion of children in the experimental group who developed the disease =
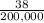 = 0.00019
= 0.00019
 = sample proportion of children in the control group who developed the disease =
= sample proportion of children in the control group who developed the disease =
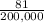 = 0.00041
= 0.00041
 = sample of children in the experimental group = 200,000
= sample of children in the experimental group = 200,000
 = sample of children in the control group = 200,000
= sample of children in the control group = 200,000
So, test statistics =
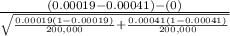
= -4.02
The value of z test statistics is -4.02.
Now, at 0.01 significance level the z table gives critical values of -2.33 for left-tailed test.
Since our test statistics is less than the critical value of z as -4.02 < -2.33, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.
Therefore, we conclude that the vaccine appears to be effective.