Answer:
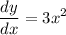
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Derivative Property [Addition/Subtraction]:
![\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]](https://img.qammunity.org/2021/formulas/mathematics/college/kqosumt4896r7x44jgtw0o7kk6g4d3irvr.png)
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Explanation:
Step 1: Define
Identify
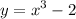
Step 2: Differentiate
- Derivative Property [Addition/Subtraction]:
![\displaystyle y' = (d)/(dx)[x^3] - (d)/(dx)[2]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/c6cdm076nzyagftn37gxjd0lfsdo6jn6ck.png)
- Basic Power Rule:
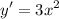
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation