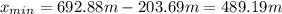Question

Suppose that a teacher driving a 1972 LeMans zooms out of a darkened tunnel at 34.5 m/s. He is momentarily blinded by the sunshine. When he recovers, he sees that he is fast overtaking a camper ahead in his lane moving at the slower speed of 15.1 m/s. He hits the brakes as fast as he can (his reaction time is 0.31 s). If he can decelerate at 2.5 m/s2, what is the minimum distance between the driver and the camper when he first sees it so that they do not collide

Answer 1

489.19m

Step-by-step explanation:

To find the minimum distance you first calculate the time in which the teacher stops:

`v=v_o-at\\\\t=(v_o-v)/(a)=(34.5m/s-0m/s)/(2.5m/s^2)=13.8s`

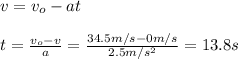
however, the reaction of the teacher is 0.31s later, then you use

t=13.8-0.31s=13.49s

during this time the camper has traveled a distance of:

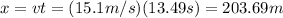`x=vt=(15.1m/s)(13.49s)=203.69m` (1)

Next you calculate the distance that teacher has traveled for 13.6s:

`x=x_o+v_ot+(1)/(2)at^2\\\\x=0m+34.5m/s(13.49s)+(1)/(2)(2.5m/s^2)(13.49s)^2=692.88m` (2)

The minimum distance between the driver and the camper will be the difference between (2) and (1):

`x_(min)=692.88m-203.69m=489.19m`