Answer:
x = -8 + 5
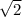 or x = -8 - 5
or x = -8 - 5
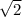
Explanation:
let u = x + 2
then (x + 2)2 + 12(x + 2) - 14 = 0 becomes:
u^2 + 12*u - 14 = 0
Quadratic Formula: u = -b/(2a) + root(b^2 - 4ac) / (2a)
u = -12/(2) + root (12^2 - 4*(-14) ) /(2)
u = -6 + root( 144 + 56) / 2
u = -6 + root(200)/2
u = -6 + 5 root(2)
or u = -6 - 5root(2)
replace u = x + 2
x + 2 = -6 + 5root(2)
x = -8 + 5 root(2) or x = -8 - 5root(2)
----------------
Do Completing the Square:
u^2 + 12 u + 36 - 36 - 14 = 0
(u + 6)^2 - 50 = 0
(u + 6)^2 = 50
u + 6 = root(50)
u = -6 + 5root(2) OR u = -6 - 5root(2)