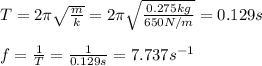Answer:
a) E = 0.52 J
b) v = 1.94 m/s
c) T = 0.129 s
f = 7.73 s^-1
Step-by-step explanation:
a) To find the total mechanical energy you use the following formula:
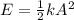 (1)
(1)
k: spring constant = 650N/m
A: amplitude of the oscillation = 4.00cm = 0.04m
you replace the values of the parameters in (1) to calculate E:
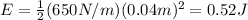
the total mechanical energy is 0.52J
b) To find the speed in the position of equilibrium you take into account that at that point all mechanical energy is kinetic energy, then, you se the following equation:
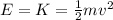
m: mass of the block = 0.275 kg
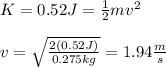
c) The period and frequency are given by: