Question

Help Me Please!!!!1

A basketball has a diameter of 14 inches. If it fits inside a cube-shaped box that has a side length of 13

inches, what is the volume, rounded to the nearest hundredth of a cubic inch, of the space inside the box

that is not taken up by the basketball?

Answer 1

The space inside the box = 2197 in³ - 1436.76 in³ is 760.245 in³.

Explanation:

Here we have the volume of the cube box given by the following relation;

Volume of cube = Length. L × Breadth, B × Height, h

However, in a cube Length. L = Breadth, B = Height, h

Therefore, volume of cube = L×L×L = 13³ = 2197 in³

Volume of the basketball is given by the volume of a sphere as follows;

Volume =
`(4)/(3) \pi r^3`

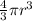
Where:

r = Radius = Diameter/2 = 14/2 = 7in

∴ Volume of the basketball =
`(4)/(3) * \pi * 7^3 = 1436.76 \ in^3`

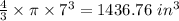
Therefore, the space inside the box that is not taken up by the basketball is found by subtracting the volume of the basketball from the volume of the cube box, thus;

The space inside the box = 2197 in³ - 1436.76 in³ = 760.245 in³.