Answer:
The equation of the hyperbola is presented as follows;

Explanation:
Here we have the standard equation of an hyperbola given as follows;
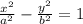
Where:
a = x intercept
The asymptote is ±(b/a)x
Since the intercept, a is ± 4, the vertices are (-4, 0) and (4, 0)
We are given the asymptote as y = 3/4x, therefore, since the genral form of the asymptote is ±(b/a)x, comparing, we have;
±(b/a)x ≡ 3/4x
We have a = ±4, therefore, b = 3
Hence the equation of the hyperbola is found by putting in the values of a and b in the general form as follows;
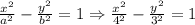
The equation of the hyperbola = x²/16 - y²/9 = 1.