Question

An undamped 2.47 kg2.47 kg horizontal spring oscillator has a spring constant of 32.8 N/m.32.8 N/m. While oscillating, it is found to have a speed of 2.30 m/s2.30 m/s as it passes through its equilibrium position. What is its amplitude AA of oscillation? A=A= mm What is the oscillator's total mechanical energy EtotEtot as it passes through a position that is 0.6520.652 of the amplitude away from the equilibrium position? Etot=Etot= J

Answer 1

0.631 m

6.53315 J

Step-by-step explanation:

m = Mass = 2.47 kg

v = Velocity = 2.30 m/s

k = Spring constant = 32.8 N/m

A = Amplitude

In this system the energy is conserved

`(1)/(2)mv^2=(1)/(2)kA^2\\\Rightarrow A=\sqrt{(mv^2)/(k)}\\\Rightarrow A=\sqrt{(2.47* 2.3^2)/(32.8)}\\\Rightarrow A=0.631\ m`

The amplitude is 0.631 m

Mechanical energy is given by

`E=(1)/(2)mv^2\\\Rightarrow E=(1)/(2)2.47* 2.3^2\\\Rightarrow E=6.53315\ J`

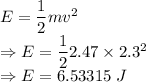
The mechanical energy is 6.53315 J