Question

The function f(x)=-(x-3)^2+9 can be used to represent the area of a rectangle with a perimeter of 12 units, as a function of the length of the rectangle, x. What is the maximum area of the rectangle?

Answer 1

Explanation:

9

Answer 2

9.

Explanation:

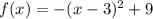`f(x) = -(x - 3)^2 + 9` is a parabola in its vertex form. For clarity, let
`f(x) = a (x - h)^2 + k` represent this function.

• 
  `a = -1`.
• 
  `h = 3`.
• 
  `k = 9`.

Note that
`a`, the leading coefficient, is negative. Therefore, this parabola opens downwards. The vertex of the parabola would be
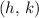`(h,\, k)`, which in this question is the point
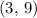`(3,\, 9)`. Since the parabola opens downwards, that vertex would be a local maximum (a crest) on its graph.

Before concluding that the maximum area of this rectangle is
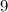`9`, make sure that
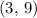`(3,\, 9)` is indeed on the graph of
`y = f(x)`.

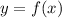The length of a rectangle should be positive. Since
`x` represents the length of this rectangle,
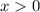`x > 0`. Also, since the perimeter should be less than
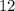`12`, the length of one side should be less than
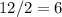`12 / 2 = 6`. Therefore, the domain of
`f` should be the open interval
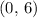`(0,\, 6)`. (Endpoints not included.)

Indeed,
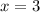`x = 3` is in that interval.
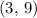`(3,\, 9)` would be on the graph
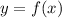`y = f(x)`. Therefore,
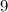`9` is indeed the maximum area of this rectangle.

Side note: if the domain is a closed interval (i.e., endpoints included,) then consider checking the endpoints, as well.