Question

Which statements about the function are true? Select two

options.
The vertex of the function is at (1,-25).
The vertex of the function is at (1,-24).
The graph is increasing only on the interval -4< x < 6.
The graph is positive only on one interval, where x <-4.
The graph is negative on the entire interval
4

Answer 1

The vertex of the function is at (1,-25)

Explanation:

I think your question missed key information, allow me to add in and hope it will fit the orginal one.

Part of the graph of the function f(x) = (x + 4)(x-6) is shown below.

Which statements about the function are true? Select two

options.

The vertex of the function is at (1,-25).

The vertex of the function is at (1,-24).

The graph is increasing only on the interval -4< x < 6.

The graph is positive only on one interval, where x <-4.

The graph is negative on the entire interval

My answer:

Given the factored form of the function:

f(x) = (x + 4)(x-6)

<=> f(x) =
`x^(2) - 2x -24`

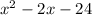
We will convert to vertex form

<=> f(x) = (
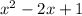`x^(2) - 2x +1`) - 25

<=> f(x) =
`(x-1)^(2) -25`

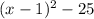
=> the vertex of the function is: (1,-25)

We choose: a. The vertex of the function is at (1,-25)

Let analyse other possible answers:

c. The graph is increasing only on the interval -4< x < 6.

Because the parameter a =1 so the graph open up all over its domain and the vertex is the lowest point.

So the graph is increasing in the domain (1, +∞)

=> C is wrong

d. The graph is positive only on one interval, where x <-4

Wrong, The graph is positive only on one interval, where x > 6

e. The graph is negative on the entire interval

Wrong, The graph is negative only on one interval, where -4< x < 6.