Question

Suppose a parabola has vertex (–8, –7) and also passes through the point (–7, –4). Write the equation of the parabola in vertex form.

a.y=(x+8)^2-7
b.y=3(x-8)^2-7
c.y=3(x+8)^2-7
d.y=3(x+8)^2+7

Answer 1

We have been given that a parabola has vertex
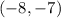`(-8,-7)` and also passes through the point
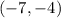`(-7,-4)`. We are asked to write the equation of the parabola in vertex form.

We know that vertex form of parabola in format
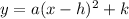`y=a(x-h)^2+k`, where point (h,k) represents vertex of parabola.

Let us write equation of parabola using our given information as:

`y=a(x-(-8))^2-7`

`y=a(x+8)^2-7`

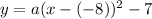
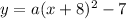
Now we will substitute the coordinates of point
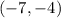`(-7,-4)` to solve for a as:

`-4=a(-7+8)^2-7`

`-4=a(1)^2-7`

`-4=a-7`

`-4+7=a-7+7`

`3=a`

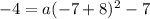
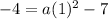
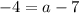
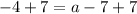
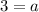
Therefore, our required equation would be
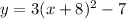`y=3(x+8)^2-7` and option 'c' is the correct choice.