Question -:
15 men can do a piece of work in 80 days. How long will it take to complete the work if 5 men are reduced?
Explanation -:
In this question we are provided that 15 men can do a work in 80 days and we are asked to calculate the time if 5 men are reduced that means we need to calculate the no. of days 10 men will take to do the same work.
There are two methods to solve this question
- Unitary Method
- Method of proportion
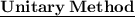
15 men can do a piece of work in 80 days
1 men can do a piece of work in 80 × 15 days
10 men can do a piece of work in
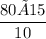 = 120 days
= 120 days
- Hence, 15 men can do a piece of work in 80 days. It will 120 days to complete the work if 5 men are reduced.

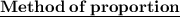
Let us assume that 10 men can do a piece of work in x days.

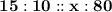
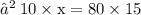

x = 120
- Hence, 15 men can do a piece of work in 80 days. It will 120 days to complete the work if 5 men are reduced.
