Question

Suppose that the duopolists Carl and Simon face an inverse demand function for pumpkins of P = 400 - Q, where Q = Qs + Qc is the total number of pumpkins that reach the market and P is the price of pumpkins. Suppose further that Simon's cost function is Cs(Qs) = Qs2 and Carl's cost function is Cc(Qc) = 30Qc + Qc2. In the Cournot-Nash equilibrium, Simon's production is

Answer 1

the Cournot-Nash equilibrium, Simon's production is 82 units

Step-by-step explanation:

The Cournot-Nash Equilibrium for Simon's production is calculated as follows:

`P = 400 - Q \\ \\ Q = Q_s + Q_c`

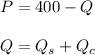
Reaction function of Carl is as follows:

Carl maximize profit at
`HR_c = HC_c`

`TR_c = P*Q_c`

`TR_c = (400 -Q_s -Q_c)Q_c`

`TR_c = 400Q_c -Q_sQ_c -Q_c^2`

⇒
`HR_c = \delta TR_c/ \delta Q_c`

`HR_c =400 -Q_s -2 Q_c`

`C_c = 30 Q_c + Q_c^2`

⇒
`HC_c = \delta C_c/ \delta Q_c`

`HC_c =30+2Q_c`

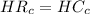
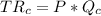
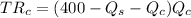
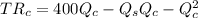
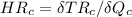
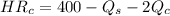
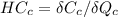
Set
`HR_c = HC_c`

`400 - Q_s - 2 Q_c = 30 - 2Q_c \\ \\ 400 - Q_s -30 = 2Q_c + 2Q_c \\\\(370 Q_s) = 4 Q_c \\ \\ Q_c = (370-Q_s)/4 \\ \\ Q_c = 92.5 - 0.25 Q_s \to Reaction \ function \ of \ Carl --- equation (1)`

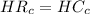
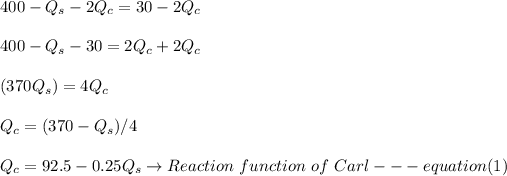
Reaction function of Simon

Since Simon maximize profit at
`HR_s = HC_s`

`TR_s = PQ_s \\ \\ TR_s = (400-Q_c -Q_s)Q_s \\ \\ TR_s = 400 Q_s - Q_cQ_s - Q_s^2`

`HR_s = \delta TR_s/ \delta Q_s`

`HR_s =400 - Q_c -2Q_s`

`C_s = Q_s^2`

`HC_s= \delta C_s/ \delta Q_s`

`HC_s=2Q_s`

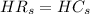
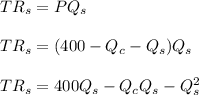
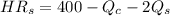
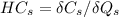
Set
`HR_s = HC_s`

`400- Q_c - 2Q_s = 2Q_s \\ \\ 400 - Q_c = 2Q_s+2Q_s \\ \\ 4Q_s = 400 - Q_c \\ \\ Q_s = (4000- Q_c)/4 \\ \\ Q_s = 100 -0.25 Q_c --- Reaction \ function \ of \ Simon \ -- equation (2)`

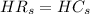
Substituting equation (1) into equation (2)

`Q_s =100 -0.25Q_c \\ \\ Q_s = 100 - 0.25(92.5-0.25 Q_s) \\ \\ Q_s = 100 -23.125 +0.0625Q_s \\ \\ (Q_s-0.0625Q_s) = 76.375 \\ \\ 0.9375 Q_s = 76.875 \\ \\ Q_s = 76.375/0.9375 \\ \\ Q_s = 82`

Thus; the Cournot-Nash equilibrium, Simon's production is 82 units