Question

One of the more famous anecdotes in the field of statistics is known as the "Lady Tasting Tea" and involves the renowned statistician Sir Ronald Aylmer Fisher. A woman claimed to be able to tell the difference in a cup of tea depending on whether or not the milk or tea was poured first. You have chosen to recreate this experience with a classmate and have fixed 40 cups of tea, of which your classmate correctly identifies 12. How large a sample n would you need to estimate p with margin of error 0.01 with 95% confidence? Use the guess p = 0.30 as the value for p. n = 42 n = 81 n = 4116 n = 8068

Answer 1

`n=(0.3(1-0.3))/(((0.01)/(1.96))^2)=8067.36`

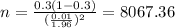
And rounded up we have that n=8068

Explanation:

The margin of error for the proportion interval is given by this:

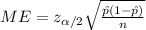`ME=z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}` (a)

We want for this case a 95% of confidence desired, our significance level would be given by
`\alpha=1-0.95=0.05` and
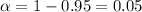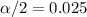`\alpha/2 =0.025`. And the critical value would be given by:

`z_(\alpha/2)=-1.96, z_(1-\alpha/2)=1.96`

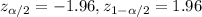
The margin of error for this case is
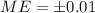`ME =\pm 0.01` and we are interested in order to find the value of n, if we solve n from equation (a) we got:

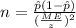`n=(\hat p (1-\hat p))/(((ME)/(z))^2)` (b)

The estimated proportion for this case is
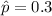`\hat p=0.3`. And replacing into equation (b) the values from part a we got:

`n=(0.3(1-0.3))/(((0.01)/(1.96))^2)=8067.36`

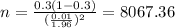
And rounded up we have that n=8068