Question

The Environmental Protection Agency (EPA) has contracted with your company for equipment to monitor water quality for several lakes in your water district. A total of 15 devices will be used. Assume that each device has a probability of 0.05 of failure during the course of the monitoring period. What is the probability that one of the devices fail?

Answer 1

36.58% probability that one of the devices fail

Explanation:

For each device, there are only two possible outcomes. Either it fails, or it does not fail. The probability of a device failling is independent of other devices. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

A total of 15 devices will be used.

This means that
`n = 15`

Assume that each device has a probability of 0.05 of failure during the course of the monitoring period.

This means that
`p = 0.05`

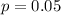
What is the probability that one of the devices fail?

This is
`P(X = 1)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 1) = C_(15,1).(0.05)^(1).(0.95)^(14) = 0.3658`

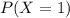
36.58% probability that one of the devices fail