Question

Associations In Data:Question 10

The list below show test scores for 3rd period on a
recent test. Finding the mean absolute deviation.
62 63 68 72 79 80 83 93 94 95
Select one:
7.8
101.2
78.9
10.12

Answer 1

`\bar X = (62+63+68+72+79+80+83+93+94+95)/(10)= 78.9`

`|62-78.9| = 16.9`

`|63-78.9| = 15.9`

`|68-78.9| = 10.9`

`|72-78.9| = 6.9`

`|79-78.9| = 0.1`

`|80-78.9| = 1.1`

`|83-78.9| = 4.1`

`|93-78.9| = 14.1`

`|94-78.9| = 15.1`

`|95-78.9| = 16.1`

`MAD = (\sum_(i=1)^n |X_i -\bar X|)/(n)`

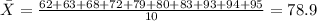
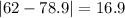
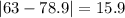
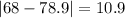
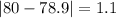
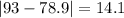
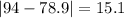
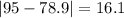
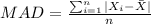
And replacing we got:

`MAD =(16.9+15.9+10.9+6.9+0.1+1.1+4.1+14.1+15.1+16.1)/(10)= 10.12`

And the best anwer is

10.12

Explanation:

We have the following data given:

62 63 68 72 79 80 83 93 94 95

And we need to begin finding the mean with the following formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\bar X = (62+63+68+72+79+80+83+93+94+95)/(10)= 78.9`

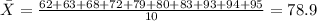
Now we can find the mean absolute deviation like this:

`|62-78.9| = 16.9`

`|63-78.9| = 15.9`

`|68-78.9| = 10.9`

`|72-78.9| = 6.9`

`|79-78.9| = 0.1`

`|80-78.9| = 1.1`

`|83-78.9| = 4.1`

`|93-78.9| = 14.1`

`|94-78.9| = 15.1`

`|95-78.9| = 16.1`

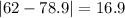
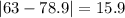
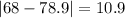
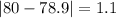
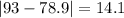
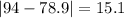
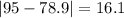
And finally we can find the mean abslute deviation with the following formula:

`MAD = (\sum_(i=1)^n |X_i -\bar X|)/(n)`

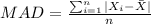
And replacing we got:

`MAD =(16.9+15.9+10.9+6.9+0.1+1.1+4.1+14.1+15.1+16.1)/(10)= 10.12`

And the best anwer is

10.12