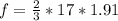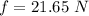Answer:
The acceleration of its center of mass is
The frictional force is
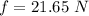
Step-by-step explanation:
From the question we are told that
The mass of the ball is
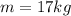
The radius of the ball is
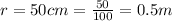
the angle with the horizontal is
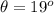
The of the ball at the base is
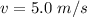
This setup is shown on the first uploaded image
looking at the diagram we see that the force acting on the ball can be mathematically evaluated as

Where f is the frictional force
The torque on the ball is mathematically represented as
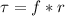
This torque can also be mathematically represented as
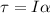
where I is the moment of inertia of the ball which is mathematically represented as
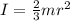
While
 is the angular acceleration which is mathematically represented as
is the angular acceleration which is mathematically represented as
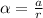
So
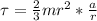
Equating the both formula for torque
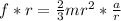
=>
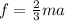
Substituting this for f in the above equation
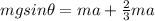
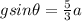
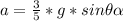
Substituting values
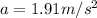
Now substituting into the equation frictional force equation