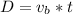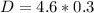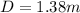Question

A string is 1.6 m long. One side of the string is attached to a force sensor and the other side is attached to a ball with a mass of 200 g. The ball is lifted to a height of 1.5 m above the ground and then released from rest. The ball swings to its lowest point where the string breaks. The ball is then in free-fall until it hits the ground. How far would the ball travel in the horizontal direction between points B and C (i.e. what is the range)?

Answer 1

bjknbjk;jln

Step-by-step explanation:

Answer 2

Complete Question

The diagram for this question is shown on the first uploaded image

Answer:

The distance traveled in horizontal direction is
`D = 1.38 m`

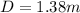
Step-by-step explanation:

From the question we are told that

The length of the string is
`L = 1.6 \ m`

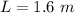
The mass of the ball is
`m = 200 g = (200)/(1000) = 0.2 \ kg`

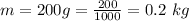
The height of ball is
`h = 1.5 \ m`

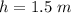
Generally the work energy theorem can be mathematically represented as

`PE = KE`

Where PE is the loss in potential energy which is mathematically represented as

`PE =mgh`

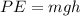
Where h is the difference height of ball at A and at B which is mathematically represented as

`h = y_A - y_B`

So
`PE =mg(y_A - y_B)`

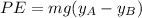
While KE is the gain in kinetic energy which is mathematically represented as

`KE = (1)/(2 ) (v_b ^2 - 0)`

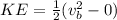
Where
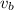`v_b` is the velocity of the of the ball

Therefore we have from above that

`PE =KE \equiv mg (y_A - y_B) = (1)/(2) m (v_b ^2 - 0)`

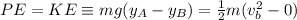
Making
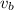`v_b` the subject we have

`v_b = √(2g (y_A - y_B))`

substituting values

`v_b = √(2g (1.5 - 0.40))`

`v_b = 4.6 \ m/s`

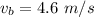
Considering velocity of the ball when it hits the floor in terms of its vertical and horizontal component we have

`v_x = 4.6 m/s \ while \ v_y = 0 m/s`

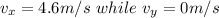
The time taken to travel vertically from the point the ball broke loose can be obtained using the equation of motion

`s = v_y t - (1)/(2) g t^2`

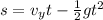
Where s is distance traveled vertically which given in the diagram as
`s = -0.4`

The negative sign is because it is moving downward

Substituting values

`-0.4 = 0 -(1)/(2) * 9.8 * t^2`

solving for t we have

`t = 0.3 \ sec`

Now the distance traveled on the horizontal is mathematically evaluated as

`D = v_b * t`

`D = 4.6 * 0.3`

`D = 1.38 m`